CCLiu 论文研读
SAR ADC 技术点迭代
Non-binary
传统二进制搜索算法的 CDAC 的 settling time 与分辨率成正比,很难将速度提上去。
请教一个关于 SARADC 的非二进制电容阵列的问题 - eetop
电容的 mismatch 带来错误的 charge redistribution 后的电压;transistor pair 的 mismatch 带来比较器的 offset,带来错误的比较结果。常用如下静态参数来衡量 ADC:微分非线性(Differential nonlinearity , DNL)、积分非线性(Integral nonlinearity , INL)、offset error、gain error。
对于理想 ADC,其输出码没变化一次,输入信号理想应增加 1LSB,但实际可能不是 1LSB,这就是微分非线性:
DNL(i)=VLSBVin(i+1)−Vin(i)−1
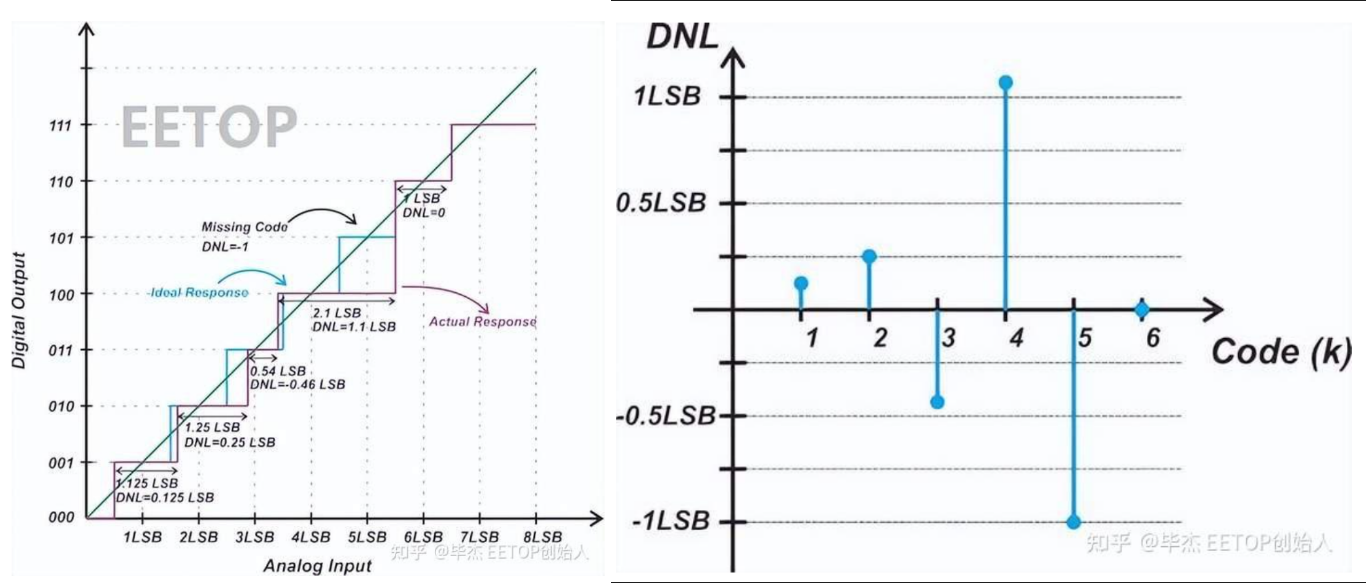
积分非线性(INL)是表征编码转换与其理想值的偏差的规范,为 DNL 的累加和。
INL(m)=i=0∑m−1DNL(i)
- offset error and gain error
offset error 是当 ADC 输入 2LSB 时,输出是否发生从 0-1 的跳变。
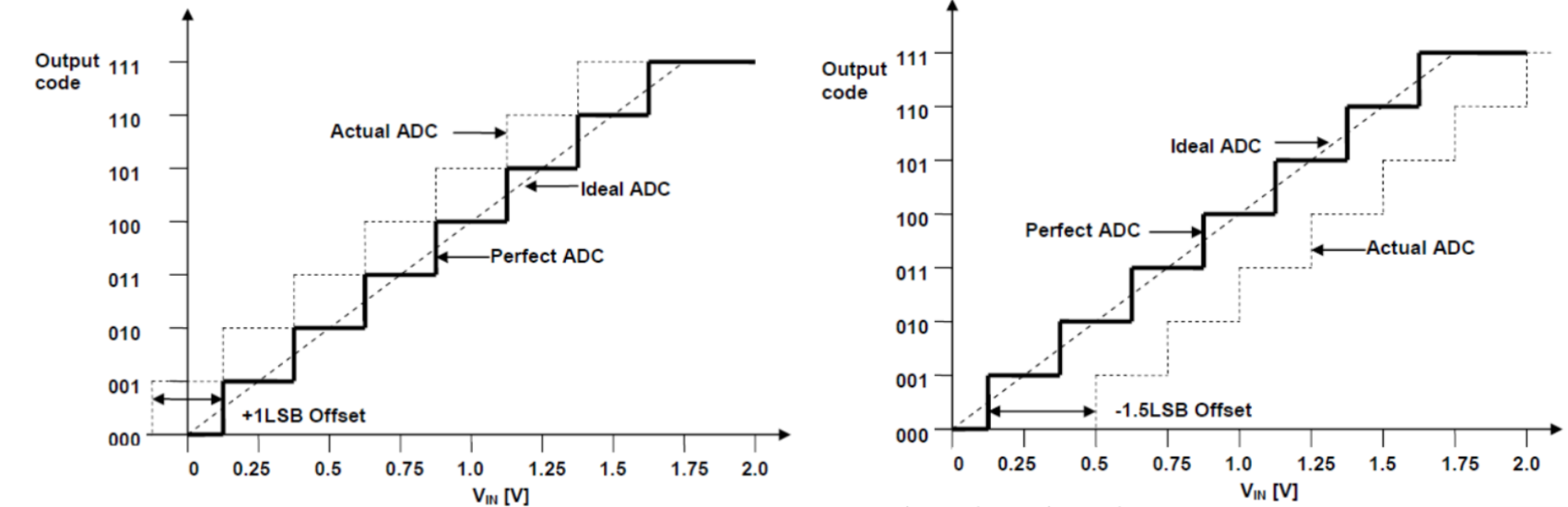
gain error 有很多校准方法,最简单的方法是两点校准,测得输出"000"和"111"的两点然后连线。
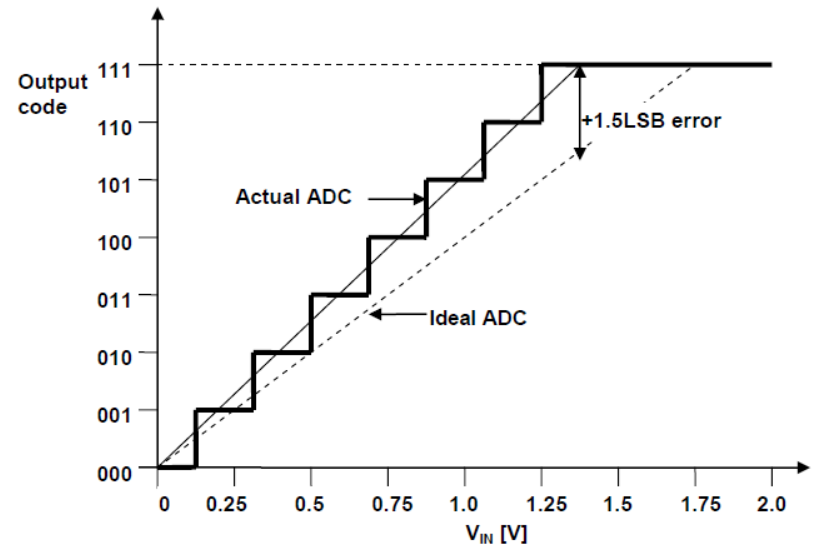
对于 3Bits ADC 时 gain error 即为输出"111"的输入模拟电压与 7LSB 之间的差值。
Non-binary search 详细分析
传统的二进制搜索算法不能容忍任何判断误差,因为没有冗余位,如果 MSB 判断错误,后面所有的 Bit 加起来都矫正不过来。但是 sub-binary is less efficient。例如传统 4Bit Binary ADC 的权重是[8,4,2,1],sub-binary 的权重可以设定为[8,2,2,1,1,1],故 sub-binary 需要 6 次比较才能实现 same resolution。对于 N-bit,M-step 的 ADC,其数字输出满足下式:
Dout=s(M)+i=1∑M−1[2⋅b[i]−1]×s(i)+[b[0]−1]
注意第 M 位是最高位,即其权重为 8;第 0 位是最低位,其权重位 1。其中 b[i] 是第 i 位的输出结果,(2⋅b[i]−1) 是将 0/1 的输出转化成-1、+1 进而来求和。由于第一位永远猜是 1,即 b(M)=1,这也是为什么 s(M) 单独在求和外面。其中 (b[0]−1) 不同于其他 bit 的求和方式是因为它的主要作用是用来微调输出结果,故采用这种简单的计算方式。
因此我们可以得到若输出结果 Dout 等于 6,则其对应多种输出的 code:
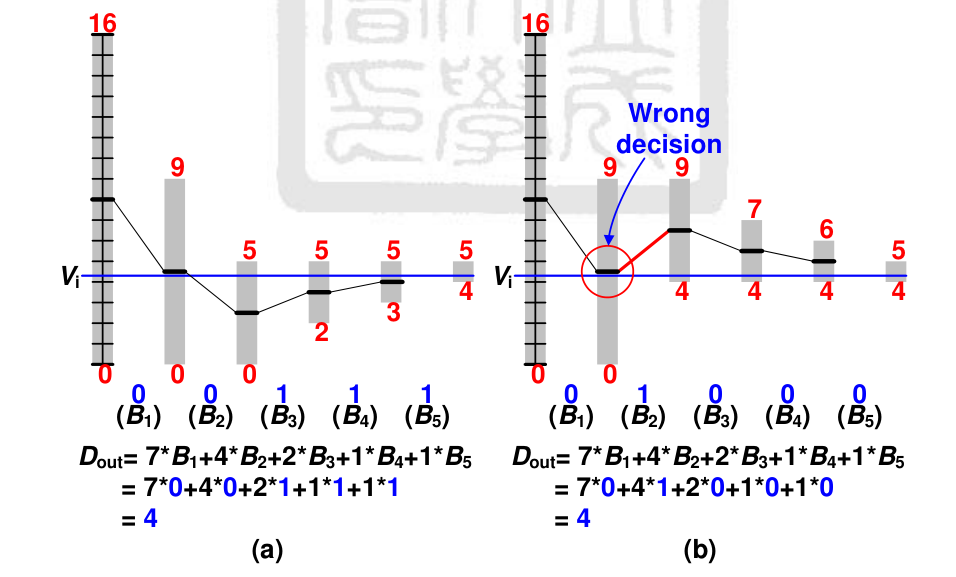
因此它可以接收某个 bit 出现判断错误即 error output,鲁棒性更好。但是它的 tolerance 并不是无限的,因此我们定义 error tolerance window ϵt,其描述的是 the range of recoverable analog voltage,如果目前的 error voltage 总和未超过 ϵt,那么在该权重的引导下,它能恢复至正确的输出值。
- error tolerance window ϵt
对于 n bit 的输出,其 error tolerance window 满足下式:
ϵt(n)=i=1∑n−2s(i)−s(n−1)
以 5bit 的[8,2,2,2,1]的权重为例,其 error tolerance window=1+2+2-2=3,因此 the range of recoverable analog voltage = [8−3,8+3]=[5,11]。
Time-interleaving
来自《Design Considerations for Interleaved ADCs》——Razavi
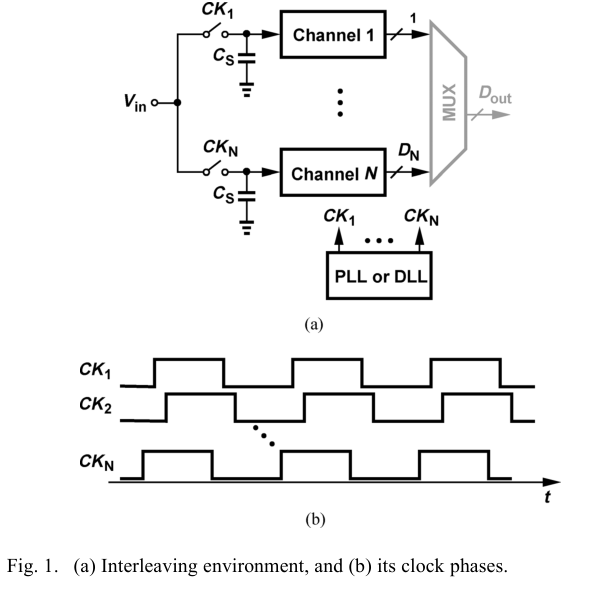
5.11 20:43 暂时看不懂,暂且先搁置
参考资料 Time-Interleaved Analog-to-Digital Converters-CSDN 博客,拉扎维先生的 JSSC
Asynchronous
对于 N bit 的 SAR ADC 需要至少 N+1 个周期完成转换(1 个采样 +N 个比较),但对于动态 latch 比较器而言,较小的 Vin 对于较小的 X、OUT 结点的电容放电电流,进而 Vout+ 和 Vout− 两节点之间的差距很难被迅速放大然后进入耦合反相器的正反馈中。即小信号比较时间较长,大信号比较时间较短。同步逻辑指的是选用最差的时间做为比较周期,但这无疑会降低 ADC 工作频率,很自然的一个想法就是当前 bit 比较完后输出一个 valid 信号,然后下一个 bit 立刻开始比较不等待,可以提升工作频率。
同时异步逻辑不需要 PLL 电路,有专门的逻辑信号产生电路。
Reduce the switching energy in CDAC
比较器和 CDAC 的功耗受 mismatch 和 noise 的限制,因此存在如下减小 CDAC 功耗的方法:split capacitor;energy-saving method;单调开关 monotonic switching 切换策略;
但是单调开关切换策略依赖于输入共模电平的 offset 会 degrade ADC 的线性度,因此提出 splitting monotonic switching 切换策略,使得 signal-dependent offset 不影响 ADC 线性度。
类似于 non-binary 方法,binary-scaled error compensation method 被提出克服 CDAC 的 settling issue,同时相较于 non-binary 方法,其需要更少的硬件和设计。
CCLiu 提出一种 predictive circuit 来避免 CDAC 中不必要的能量消耗,在不影响运行速度的情况下减小功耗同时提高线性度。
Chapter2 开关的单调切换策略
在 charge-redistribution 结构中,capacitor 网络同时担任 S/H 网络和 CDAC 阵列的作用。
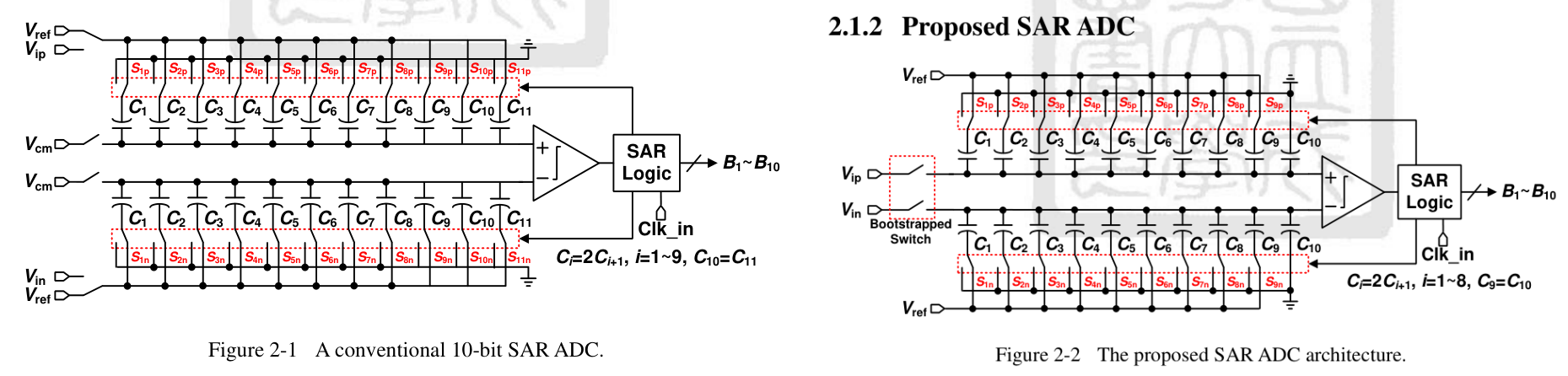
Conventional CDAC
以上半部分电容阵列为例:采样阶段,电容下极板充电至 Vip,上极板被置位到 Vcm,然后 MSB 位对应的最大的电容 C1 上极板由 Vip 切换到 Vref,同时其他电容接地。具体分析参考下方链接:
CCLiu adc 论文中开关电容切换时的能量消耗的详细计算 - EETOP
Proposed CDAC
上极板采样 → 提高速度又拓展带宽;下极板最开始统一置位到 Vref;当 ADC 关闭自举开关(即结束采样后),比较器直接开始工作,不需要像传统结构那样将上极板由 Vip 切换到 Vref 然后再开始比较:
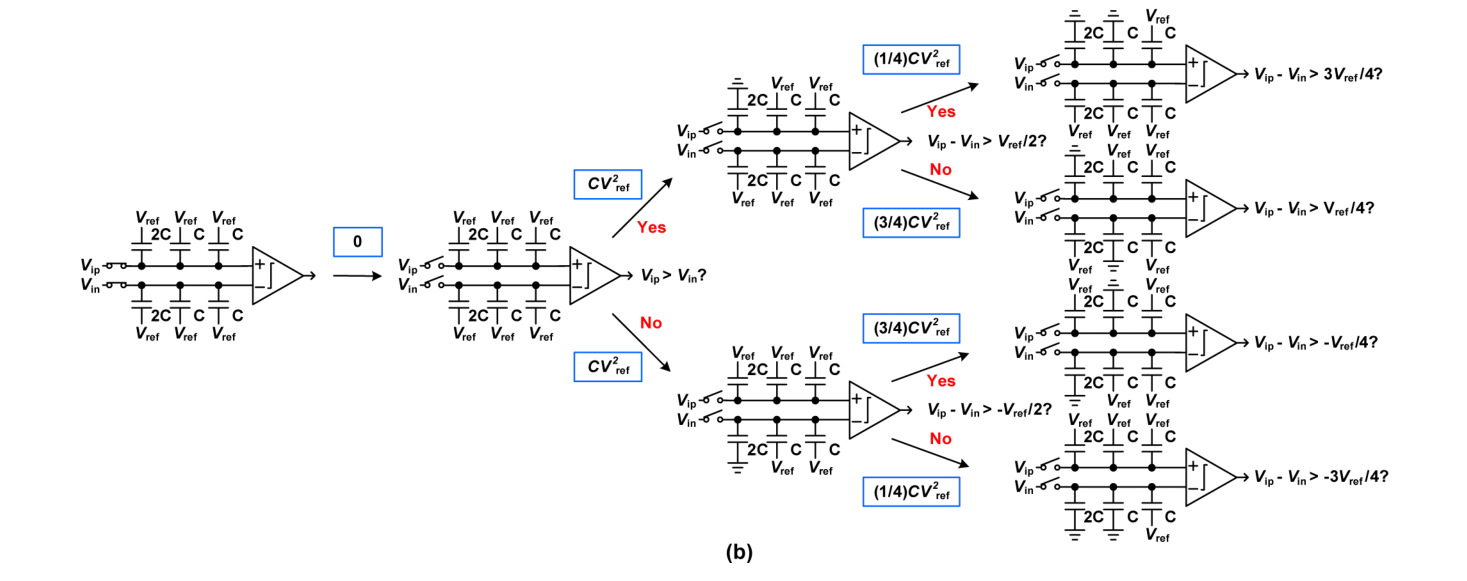
Qp(0)Qn(0)=4C⋅(Vip−Vref)=4C⋅(Vin−Vref)
采样结束后直接开始比较:
Vp(1)Vn(1)=Vip=Vin
第二步比较过程:
Qp(1)Qn(1)=2C⋅(Vp(1)−Vref)+2C⋅(Vp(1)−0)=4C⋅(Vin−Vref)
根据电荷守恒求解 Vp(2,up):
Vp(2,up)Vn(2,up)=Vip−21Vref=Vin
进而实现 Vip−Vin>?21Vref 的比较。
Vcomp,pVcomp,n=(C1+...+C9)⋅(Vip−Vref)+C10⋅Vip==(C1+...+C9)⋅(Vin−Vref)+C10⋅Vin
过程消耗能量的比较:
Eavg,convEavg,mono=i=1∑n2n+1−2i(2i−1)CVref2=i=1∑n−1(2n−2−i)CVref2
由于 ADC 输出每个 code 的概率一致,因此我们需要对输出所有 code 的能量总和取平均。若以 10-bit 为例,则代入得:
Eavg,convEavg,mono=i=1∑10211−2i(2i−1)CVref2=i=1∑10(211−i−211−2i)CVref2=[211⋅(1−2101)−211⋅31]CVref2=1363.3CVref2=i=1∑9(28−i)CVref2=28⋅(1−291)CVref2=255.5CVref2
其中 Eavg,conv 在原文中给出的是 1365.3CVref2,推测可能是忽略了 2101,不过并不影响两种切换策略的能量消耗之间存在数量级的差异。也有人指出这是类 Vcm-based 切换策略。
Bootstrapped switch design
参考之前写的自举开关报告
Comparator design
proposed latch-based dynamic comparator,结构如下图所示:
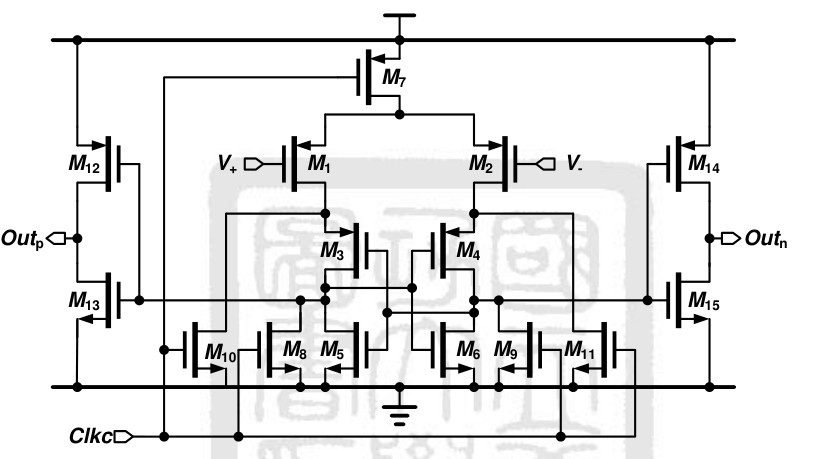
就是 strong-arm latch+ 输出结点的反相器。
不过不同于它是 nmos 输入,但是 pmos 的 1/f 噪声更小,不知道为什么这样选?
SAR ADC control logic
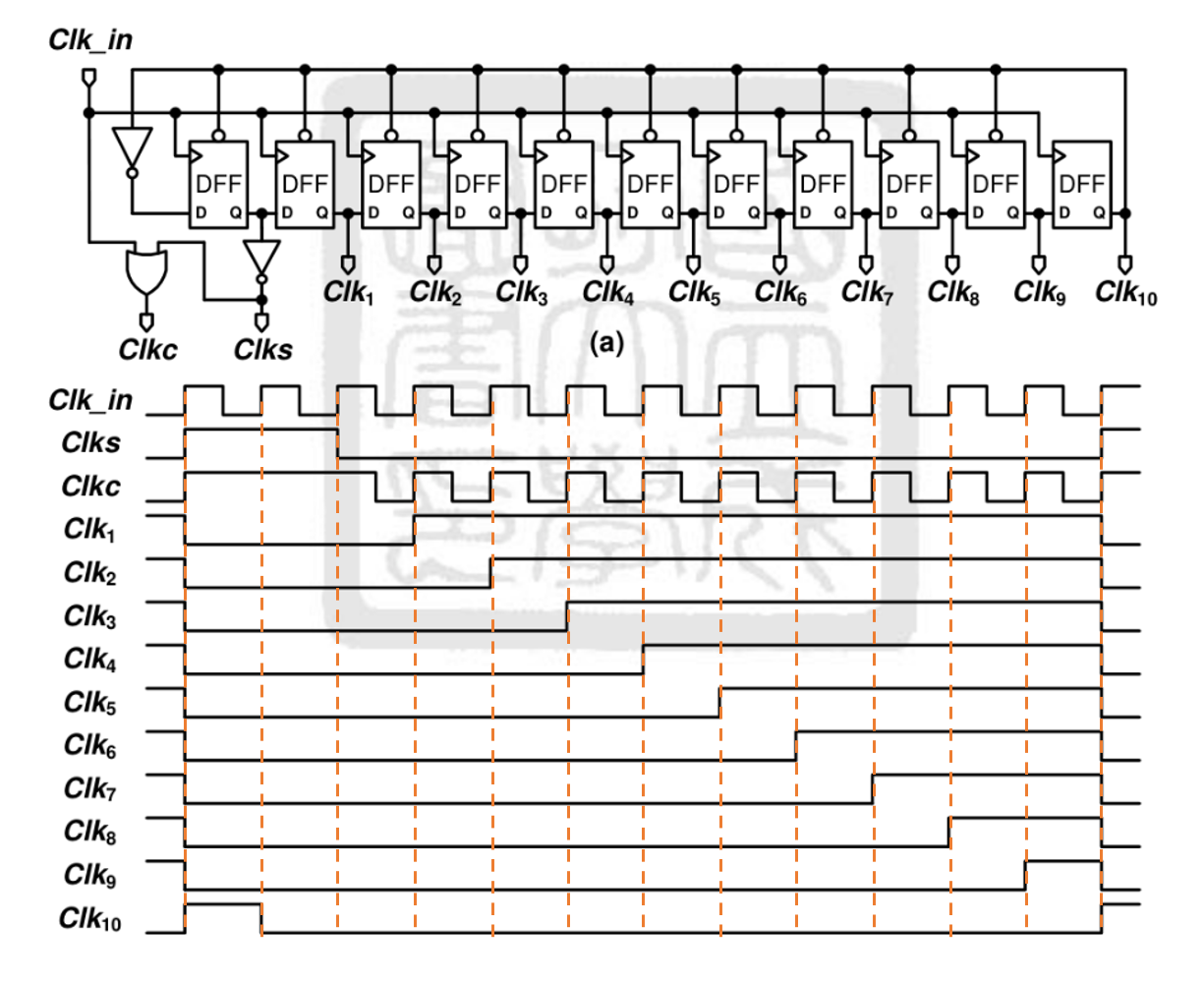
D Flip-flop 当 CLK_in 上升沿到来时,输出 Q=D;
diagram 分析
注意前 10 个 D Flip-Flop 具有一个低电平使能端;
❌:因此当前 10 个 D Flip-Flop 的使能端输入低电平时,其输出 复位,输出 0;但 CLK(9)初值为高,则 CLK10 输出高,进而我们将 CLK(10)做为前 10 个 D Flip-Flop 的使能信号控制信号;下一个时刻 CLK(10)读入 CLK9 复位后输出的低电平,进而前 10 个 D Flip-Flop 脱离复位状态,进入正常工作状态。
✔:当前 10 个 D Flip-Flop 的使能端输入低电平时,其 正常工作,即上升沿到来时 Q(n+1)=D(n);CLKs=CLK(0)
- CLK_in-1:先采样: CLK_in 第一个上升沿到来时,DFF(1)-DFF(10)被置位输出低电平,因此 CLKs=Q(1)=1;CLK(1)-CLK(9)输出低电平,CLK(10)输出高电平;
- CLK_in-2:CLK(0)读入 CLK(10)=0,故此时 CLK(0)-CLK(10)均输出逻辑 0;故 CLKs=Q(1)=1;CLKc = CLKs ∪ CLKin=1;
- CLK_in-3:CLK(0)读入 CLK(10)=1,故此时 CLKs=0,故 CLKc=CLK_in,因此 CLKc 在这个周期内一半时间高电平、一半时间低电平;且 CLK(1)-CLK(10)均为逻辑 0
- CLK_in-4:CLK(0)读入 CLK(10)=1,CLK(1)读入 CLK(0)=1;同时 CLK(2)-CLK(10)均为逻辑 0;CLKc=CLK_in,故一半时间高电平、一半时间低电平;
- 后面的周期类似,逐 bit 读入逻辑 1;
Capacitor Array
10Bits ADC 共需 29 个 unit capacitor;

10-bit 50MS/s SAR ADC design
S/H circuit
由于 Cds 的存在(典型值 5fF),输入信号会耦合至采样电容上,耦合作用恶化了自举开关的高频性能,因为 Cds 在 comp 阶段中会带来 unequal 的电荷注入,这会带来一个 dynamic offset。因此采用一个交叉耦合的 mom 电容来减小该作用的影响至 <21LSB,若想实现更高的准确度,dummy switchs 和 dummy routing 也是一种方法来抑制作用。
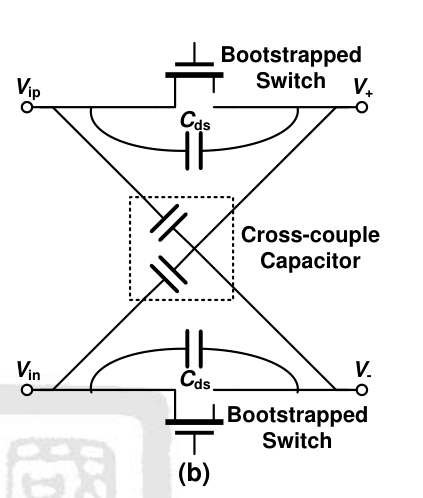
感觉就是互补开关管的思想
Dynamic Comparator
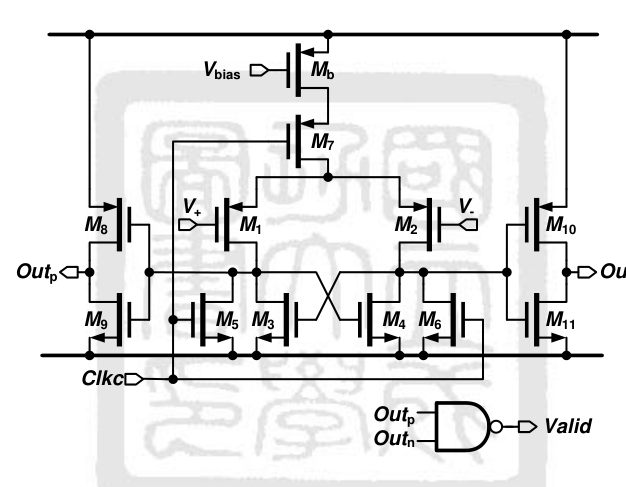
感觉就是 strong-arm 结构的比较器,只不过它是 pmos 输入,可能是为了减小1/f噪声?,然后输出端加了一个反相器以保证正确的输出比较结果,但是我加了三个比较器,希望增强驱动能力?
同时作者提出该结构的 offset voltage 满足下式:
Vos=ΔVTH1,2+2(VGS−VTH)1,2(S1,2ΔS1,2+RΔR)
其中 S=W⋅L;R 是负载电阻;其中第一项 ΔVTH1,2 是 static offset,并不影响 SAR ADC 的 performance;第二项是依赖于 signal 的 dynamic offset。
并且通过添加 Valid=Outn∩Outp,即如果有逻辑 0 则输出 1,进而便于后续实现异步逻辑。
减小 offset 的方法:
- 提升 comparator 尺寸,但会增大功耗;
- 减小输入管的 effective voltage(感觉是过驱动电压),但会降低速度;
- 采用 error tolerant non-binary search 算法;
-
增加Mb以形成cascode结构,保障稳定的漏极电流;
6-bit 220-MS/s Time-Interleaving SAR ADC
应用场景:硬盘驱动、本地网络需要高速 ADC,但是精度 6-bit 足够;因此考虑 异步逻辑+时间交织;
- 由于 SAR ADC 常过采样,因此高频工作的 SAR 需要 2 倍频率的时钟,提出时间交织技术即为了避免使用高频时钟;
但并行转换器数量的增加会带来功耗和面积的增加。
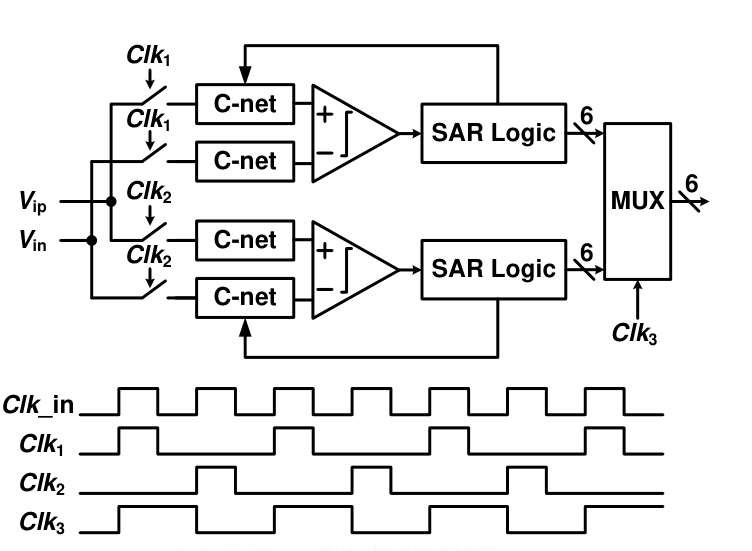
Comparator design
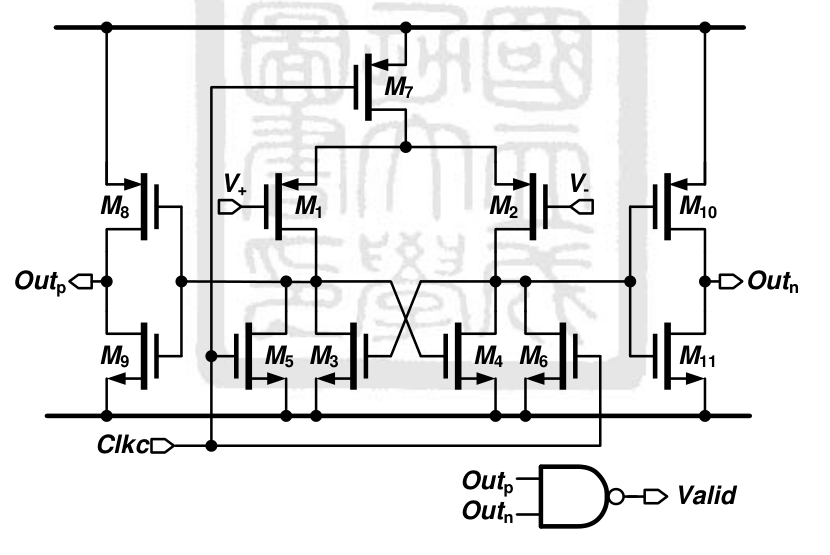
为减小两个 sub-ADC 的 channel mismatch,调整比较器的 offset 满足 <61LSB,同时要注意 layout 共质心布局,且无 dc 电流和静态功耗。
Q:不同于上一个 ADC 的 comparator 的原因?
A:上一个 ADC 是 10-bit,它对 offset 的要求更高,这个 adc 只需要 <61LSB 即可,因此不需要添加 Mb 构成 cascode 结构稳定漏极电流。
SAR Logic Design
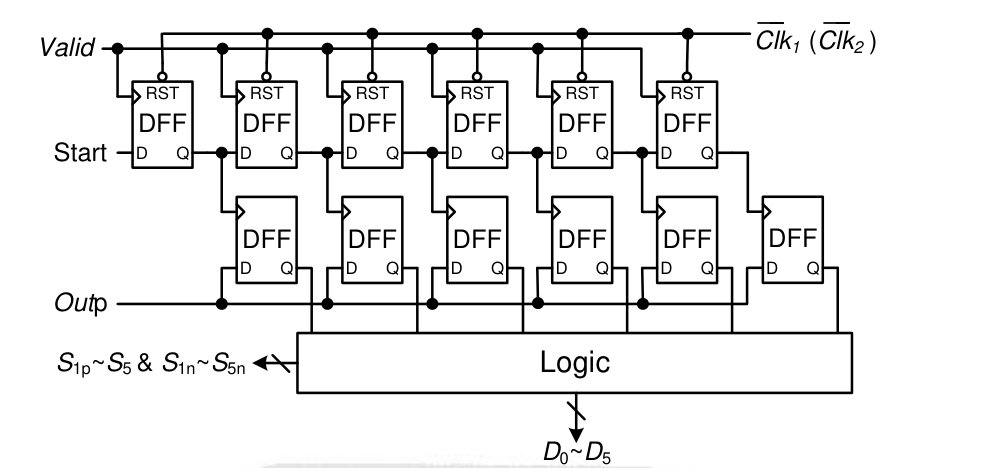
仍然为单调开关切换策略,利用 Valid 信号的上升沿做为 DFF 的 CLK;
高速 SAR ADC 的 Binary-Scaled Error Compensation
传统的 Binary Search:
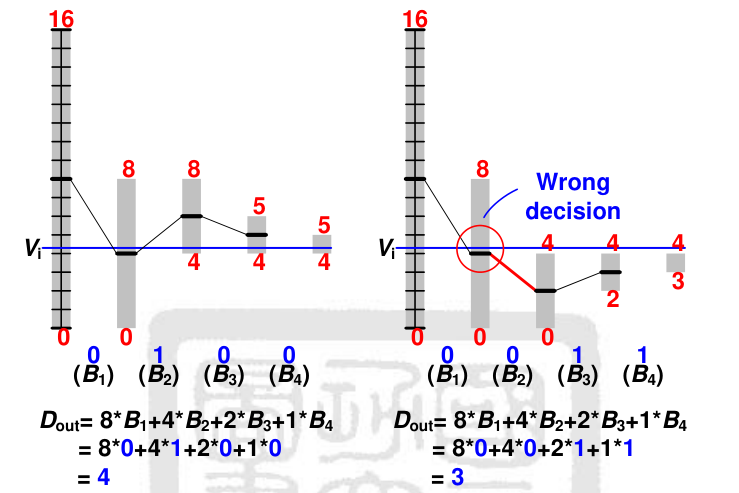
传统的二进制搜索算法 一旦出现错误判断的bit,即使后续所有的 bit 全部翻转也无法纠正。导致比较器判断错误的原因很多:comparator 的 metastability issue;thermal noise;supply voltage noise;采样频率过高导致 DAC 阵列来不及 stabilize;
Non-binary Search
参考下方跳转内容:
Non-binary search 详细分析
Proposed Binary Search with Error Compensation
判断过程如下图所示:
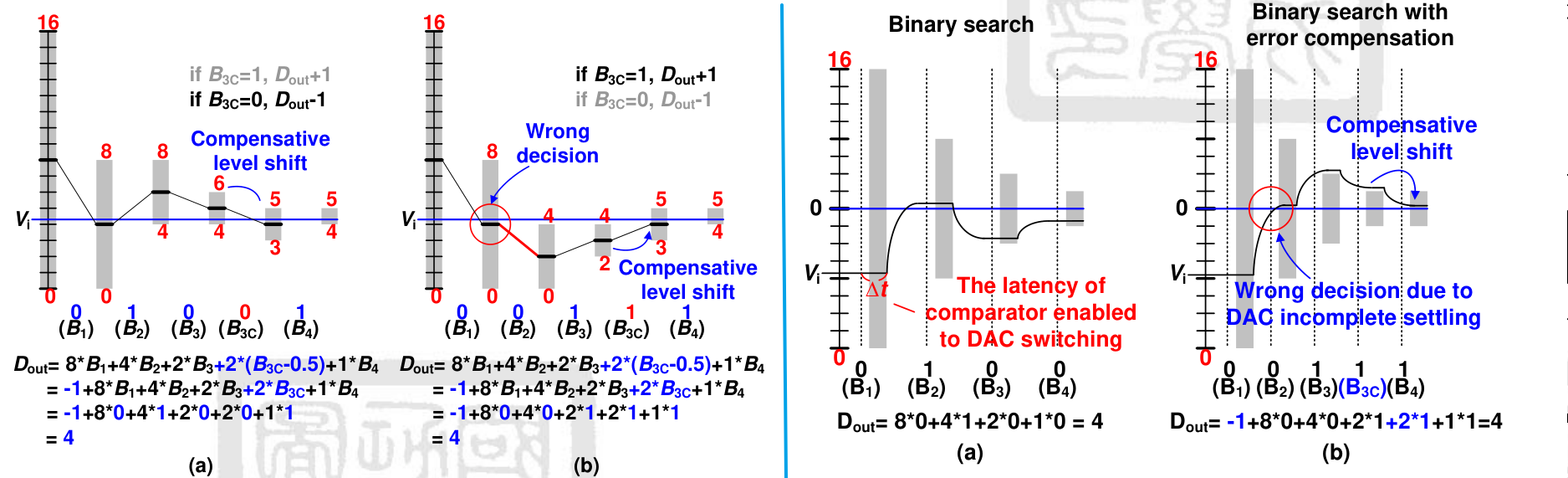
如 Right Fig 所示,当 B1 判断结束后,Vref 切换后 Ccomp,+ 和 Vcomp,− 没能在 B2 开始判断前 stabilize,进而导致判断错误。
增加了一个补偿 bit 来纠正错误的输出 code,补偿的 bit 权重=LSB;对于补偿 bit 常规的 0/1 求和输出是有问题的,它永远是非负的,因此不能纠正另一个极性的错误,因此我们采用 2⋅(B3C−0.5) 来求和输出。即当 B3C=1 时实际值为 1,当 B3C=0 时实际值为-1,可以实现两个极性的错误都可以纠正。
10-bit 100-MS/s SAR ADC with binary 权重补偿
S/H 电路 +CDAC 阵列 + 比较器结构如下图所示:
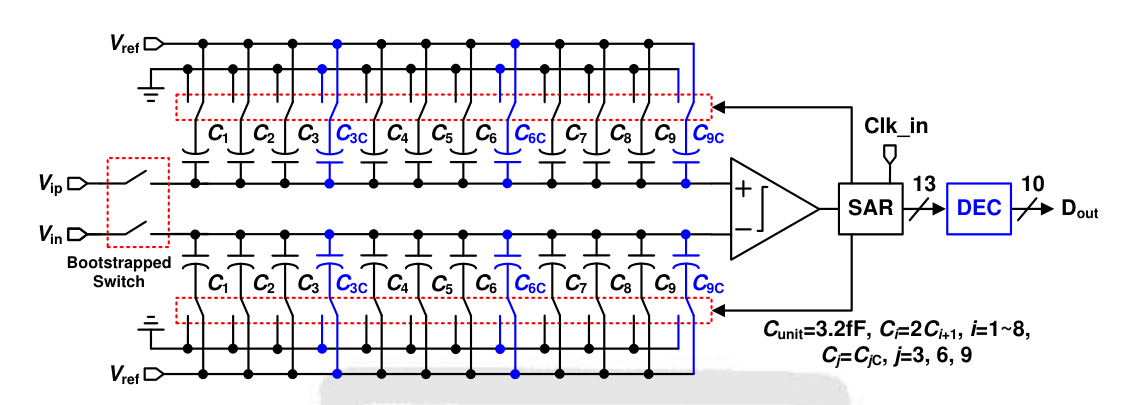
- Q:它为什么每 3 个 bit 加一个补偿矫正 bit 呢?
A:从 Proposed Binary Search with Error Compensation 的图中来看,每 3 个 bit 一个补偿矫正 bit 可以矫正至多 MSB-1 为的判断错误,即错误结果与实际结果至多相差 2LSB(注:此处的 LSB 并非全部 10bit 的 LSB,而是每一个分组的电容阵列的 LSB),参考 SAR ADC 输入范围以及二进制冗余方法 - eetop。但是作者也在文中提出 three compensative cycles achieves the shortest conversion time,同时 3 个补偿电容带来了 至多12.5%的tolerance。
这种补偿方法也可以移植到 non-binary 的 CDAC 阵列中,但是 binary-scaled 的 CDAC 的 layout 相对更容易 matching。
Digital Error Correction Logic
该电路的作用是 converts the 13-bit redundant codes to 10-bit binary codes。这 13-bit 冗余位的权重分别为:
512,256,128,128,∣64,32,16,16,∣8,4,2,2,1
则 output 满足下式:
output=512×B1+256×B2+128×B3+128×(B3c−0.5)=64×B4+32×B5+16×B6+16×(B6c−0.5)=8×B7+4×B8+2×B9+2×(B9c−0.5)
因此共计 offset 满足下式:
offset=128×(−0.5)+16×(−0.5)+2×(−0.5)=−73
因此数字误差校正逻辑如下图所示:

A:以后三个 bit 为例,定义 Di=Resi+Bi,因此有:
当 B10=0,则 D10=1;当 B10=1,则 D10=0,同时进位 1,故 D10=B10;
当 B9c=0 时,Res9=1+0=1;当 B9c=1 时,Res9=1+1 进位,因此 Res9=B9c;
当 B9c=0 时,Res8=1+0;当 B9c=1 时,Res8=1+1 进位,因此 Res8=B9c;
当 B9c=0 时,Res7=0+0;当 B9c=1 时,Res8=0+1 进位,因此 Res8=B9c;
剩下的 bit 也同理,将上述逻辑表达式转化成电路图(数字电路)后如下图所示:
因此数字误差校正电路如下图所示:包含 5 个反相器 +9 个全加器
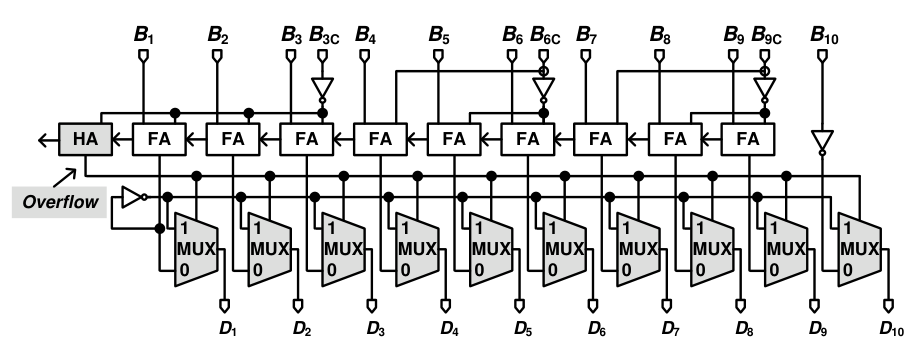
FA:Full adder;HA:Half adder;MUX:Multiplexer;
Summary
本 chapter 提出的 binary-scaled error compensation method 主要是为了解决高速 ADC 中 DAC的settling issue问题。该电容补偿方法对 non-binary search 同样适用。
Splitting Monotonic Capacitor Switching Procedure
Chapter2 提出的单调开关切换策略相较于传统切换策略实现了更高能效同时减少了一半的电容数量。但是输入共模电压的变化带来的比较器的 offset 降低了 ADC 的 performance,因此本 chapter 提出一种 splitting monotonic switching procedure 来 maintain VCM during bit cycling。同时在 DAC 网络中采用 预测电路 以减少不必要的开关,这个预测电路由两个 coarse comparators 和 sub-ADC 组成。该 method 进一步节约了 comparator、CDAC 的能耗,同时提高了运行速度及 SAR ADC 的线性度。
下方为单调开关和分离单调开关的结构、切换策略:
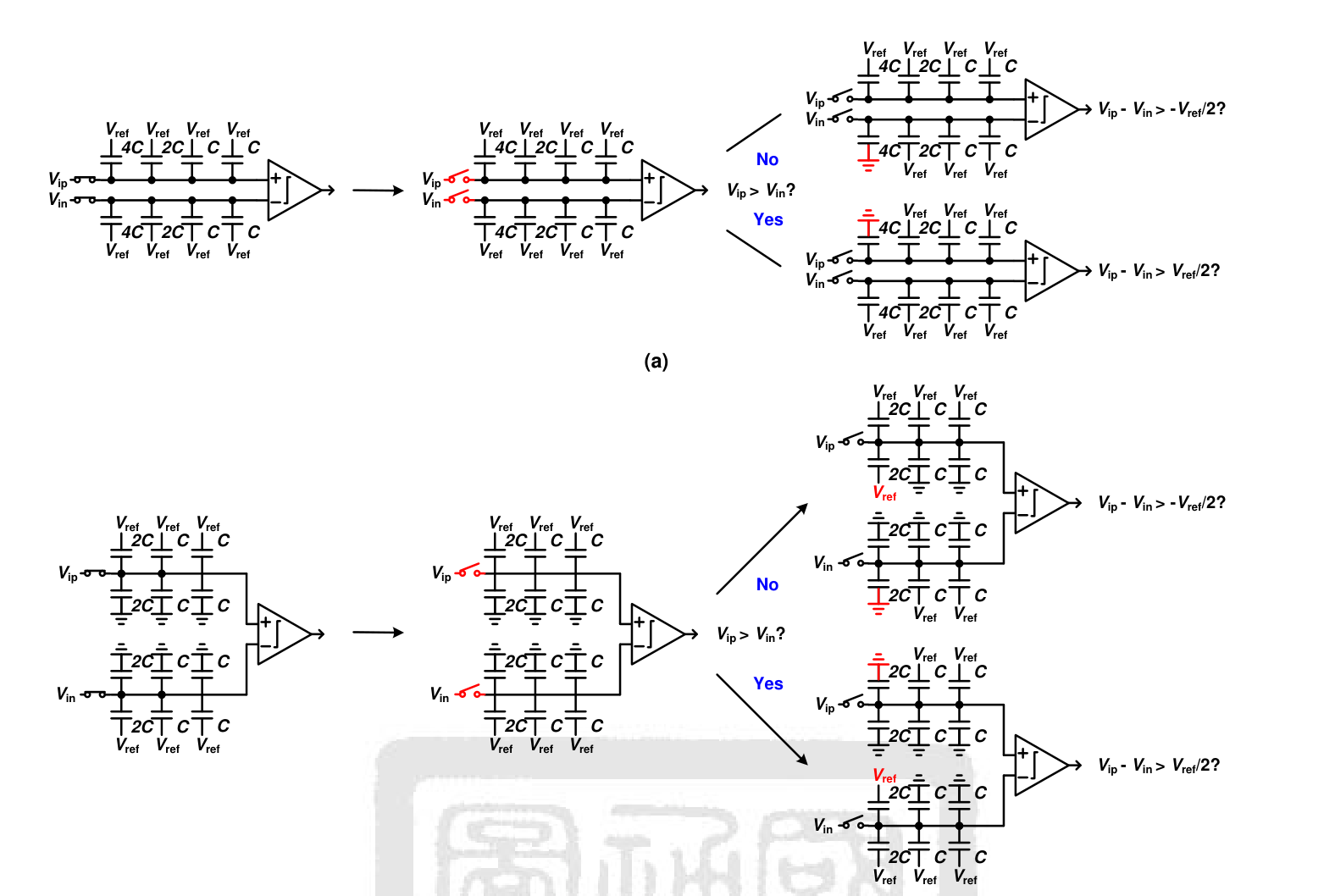
在第 0 次,由于是采样因此有:
Vp(0)Vn(0)=Vip=Vin
因此比较器各端口电荷量满足下式:
Qp(0)Qn(0)=4C⋅(Vip−Vref)+4C⋅(Vip−0)=4C⋅(Vin−Vref)+4C⋅(Vin−0)
断开 Vip 连接后,进行第一次比较,如果 Vip>Vin ,则向下切换,切换后各端口电荷量满足下式:
Qp(1)Qn(1)=(C+C)⋅(Vp(1)−Vref)+2C⋅(Vp(1)−0)+4C⋅(Vp(1)−0)=(C+C)⋅(Vn(1)−0)+2C⋅(Vp(1)−Vref)+4C⋅(Vn(1)−Vref)
根据电荷量守恒即 Qp(0)=Qp(1), Qn(0)=Qn(1) 得到下式:
Vp(1)Vn(1)=Vip−41Vref=Vin+41Vref
进而实现对 Vip−Vin>?21Vref 的判断。
同时对于 monotonic switching procedure,其输入共模电平单调下降,以第三次切换后为例,其比较器各输入端口电压满足下式:
Vp(3)Vn(3)Vcm(now)=Vcm−Vip+81Vref=Vcm−Vin+87Vref=21(Vp(3)+Vn(3))=Vcm+21Vref
注:此处我怎么算出来共模电平持续增加了,我就请问了?
但对于 splitting monotonic switching procedure 来说,其共模电平会逐渐趋近于 Vcm,两种切换策略对比图如下图所示:
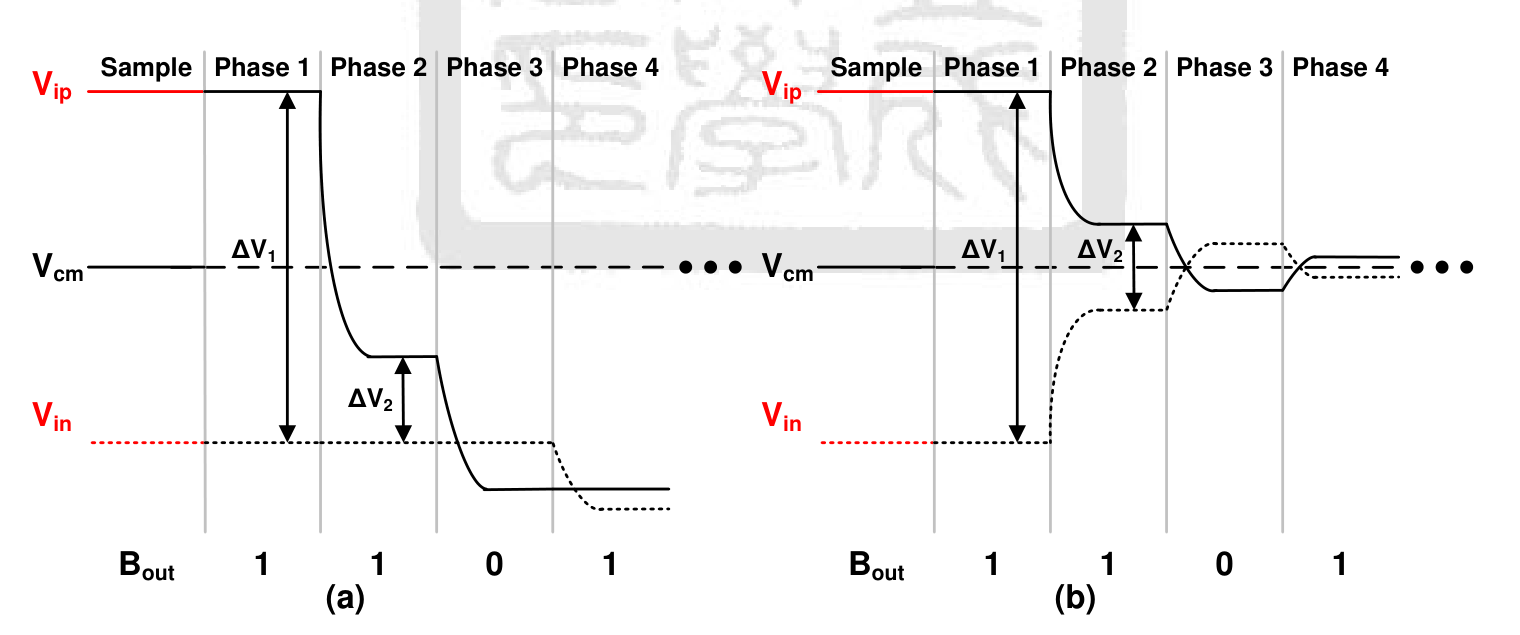
Predictive Capacitor Switching Procedure
传统的 SAR ADC 是 binary-search algorithm,特别地当外加大电压的同时伴随着 small difference,这会带来不必要的能量消耗。下面是刘纯成博士的 idea:
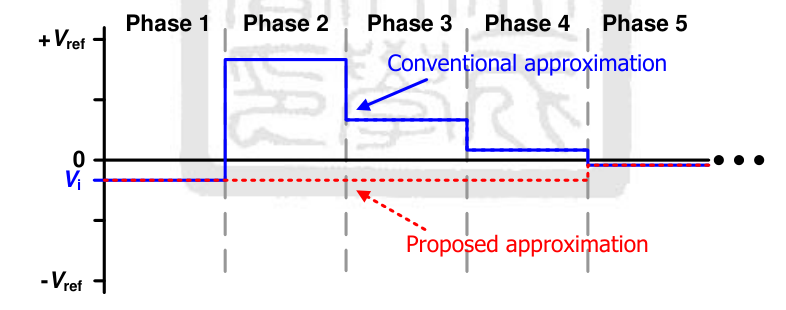
刘纯成博士的想法是:保持 bit cycling 操作直至差值 <21LSB,进而再去 add or subtract 电压。
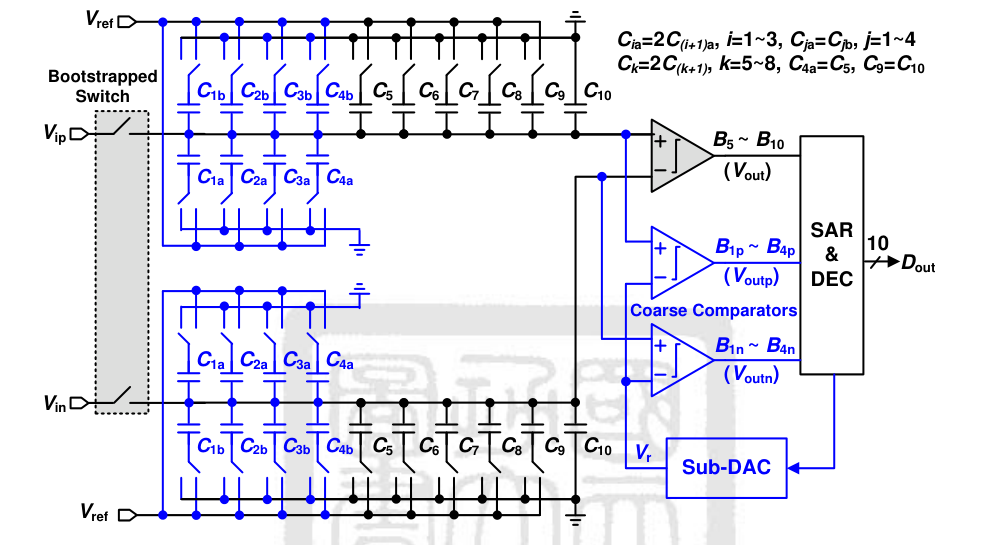
综合考虑到效率和能效,因此 CCLiu 选择前 4bit MSB 用 Splitting Monotonic Capacitor Switching Procedure,后面 6 bit 用 Monotonic Capacitor Switching Procedure。
此时 coarse comparator 的判断阈值 Vr 的选择即参考它的精度即可,考虑到 C5=16Cunit,因此取 Vr=21WeightC5=8LSB 即可。
idea总结:在由 Splitting Monotonic Capacitor Switching 的电容决定的精度下,设定该切换策略所对应的 CDAC 的 41LSBequal 为电容开关开始切换的临界阈值,在输入信号差值小于 41LSBequal 后再实行开关的切换,实现比较速度的提升和能效的提高。
特别地在 10-bit 的精度下,比较器 dynamic offset problem 的影响几乎可以忽略。下面我们来讨论一下刘纯成博士在这个 ADC 中提出的 digital error correction logic(仅包含 4 个全加器):
注意由于我们取的临界阈值电压是 41LSBequal,因此我们需要同时利用两个 coarse comparator 的比较结果;或者说 Bin 是 Vin?<Vr 的判断结果,Bip 是 Vip?>Vr 的判断结果,因此二者加起来就是 Bin+Bip=
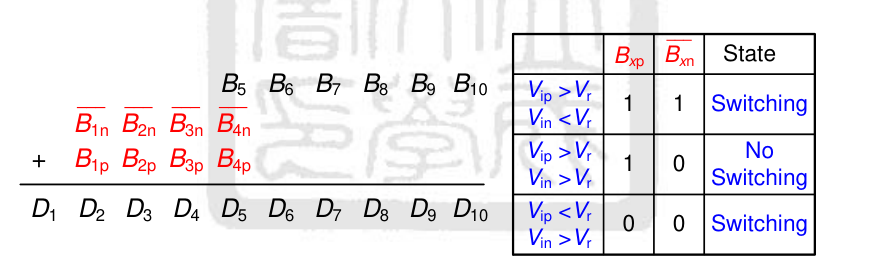
- 以 D1 为例:B1n=1⇒Vin<Vr 并且 B1p=1⇒Vip>Vr,因此当且仅当 B1n=B1p=1 时,有 D1=1;
- D2:
一个 bit 一个 bit 的分析:
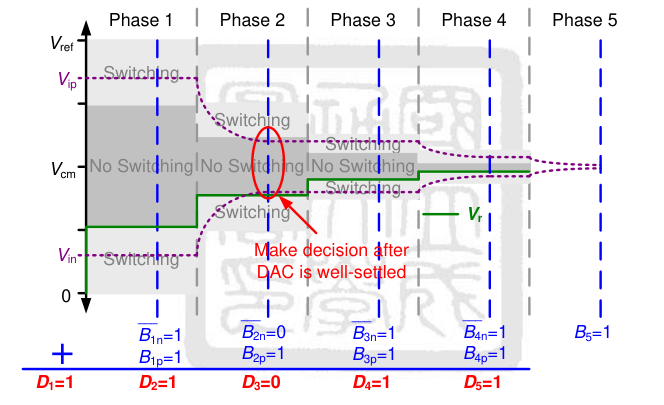
coarse comparator 各输入端口电荷量满足下式:
Qp(0)Qn(0)=(C1b+C2b+...+C10)⋅(Vip−Vref)+(C1a+C2a+...+C4a)⋅(Vip−0)=(C1b+C2b+...+C10)⋅(Vin−Vref)+(C1a+C2a+...+C4a)⋅(Vin−0)
各输入端口电压满足下式:
Vp(0)Vn(0)=Vip=Vin
此时 Vr 选定为 4Vref,即判断
B1pB1n=(Vip>2Vref)?=(−Vin>−2Vref)?1:01:0
如果有 Vip>2Vref 且 Vin<2Vref,则输出 code 有 D1=1;该条件等价于 B1p=1 同时 B1n=1。

























