半导体物理半期考试参考解析
四川大学期中考试试题(开卷) (2024 - 2025 学年第 1 学期) A 卷
课程名称:半导体物理 任课教师:杨治美
2024 年 11 月 25 日
1 题目
-
${L}{n}(E) = ( )$ , ${L}{D} =( )$ 。
-
半导体中过剩电子浓度为 $ \Delta n = {10}^{15} cm^{-3} $ ,过剩载流子的寿命为 $ \tau_{n0} = {10}^{-6}s $ 。在 $ t = 0 $ 时, 产生过剩载流子的外部作用停止,因此 $ t > 0 $ 时半导体恢复到平衡状态, $ t = {4\mu s} $ 时的过剩载流子的复合率 ( )。
-
假设两块半导体材料 $\mathrm{A}$ 和 $\mathrm{B}$ 除了禁带宽度不同,其它参数完全相同。 $\mathrm{A}$ 的禁带宽度是 $ 1.0eV $ , B 的禁带宽度是 $1.2eV$,${300}\mathrm{K}$ 时两种材料的 ${n}_{i}$ 的比值是( )。
-
特定半导体内存在三种散射机制,只存在一种散射机制时的迁移率为 $\mu_{1}=2000cm^{2}/(V\cdot s)$ ,只存在第二种散射机制时的迁移率为 $\mu_{2}=1500cm^{2}/(V\cdot s)$ ,只存在第三种散射机制时的迁移率 $\mu_{1}=2000cm^{2}/(V\cdot s)$ ,只存在二种散射机制时的迁移率为 $\mu_{3}=500cm^{2}/(V\cdot s)$,总的迁移率为( $\quad$ )
-
最有利效的复合中心能级位置在 ( ) 附近;最有利陷阱作用的能级位置在 ( ) 附近, 常见的是 ( ) 陷阱。
A. ${E}{A}$ B. ${E}{D}$ C. ${E}{F}$ D. ${E}{i}$ E. 少子 F. 多子
- 当一种 $\mathrm{n}$ 型半导体的少子寿命由直接辐射复合决定时,其小注入下少子寿命正比于( )。
A. $\frac{1}{n_{0}}$ $\quad$ B. $\frac{1}{\Delta n}$ $\quad$ C. $\frac{1}{p_{0}}$ $\quad$ D. $\frac{1}{\Delta p}$
- 以下 4 种半导体最适合制作高温器件的是( )。
A.Si $\quad$ B.Ge $\quad$ C.GaAs $\quad$ D.GaN
二、根据对 (Si) 晶体结构基本认识, 尝试回答以下问题: (10 分)
-
试画出 (Si) 的晶体结构图;
-
试比较 (100)、(110) 和 (111) 面密度的大小, 要求写出详细计算过程;
-
MOSFET 器件和 NPN 晶体管制造过程中, 会分别选用那种晶向的衬底, 为什么?
三、谈根据所学知识, 谈谈你对晶体中缺陷的认识。(10 分)
四、讨论杂质浓度和温度分别对禁带宽度、迁移率、电阻率的影响。(10 分)
五、描述直接复合与间接复合的物理过程。为什么只有深能级才能起到有效复合中心的作用? 说明掺Au后寿命为什么会明显下降?(10 分)
六、何谓少子寿命?决定半导体少子寿命的主要因素有哪些,并说明原因?写出三种或三种以上少子寿命检测的方法, 并简要说明基本测试原理(15 分)
七、一 $\mathrm{n}$ 型半导体样品,复合能级 ${E}{t}$ 在导带底之下三分之一 ${E}{g}$ 处,设 ${\tau }{n}$ 和 ${\tau }{p}$ 为同一数量级, 并且与温度无关。试根据复合中心理论讨论寿命与温度的关系, 并根据得出的结果, 说明复合中心能级 ${E}_{t}$ 位置的方法。(25 分)
2 参考解析
1. $ { L } _ { n } ( E ) = $ (电子牵引长度) , $ { L }_{ D } = $ (德拜长度)。
解: ${L}{n}\left( E\right)$ 是电子牵引长度,其中下标 $\mathrm{n}$ 表示电子,要同 ${L}{n}$ 电子扩散长度区分; ${L}_{D}$ 是德拜长度。
2. 半导体中过剩电子浓度为 ${\Delta n} = {10}{15}{\mathrm{cm}}{-3}$ ,过剩载流子的寿命为 ${\tau }_{n0} = {10}^{-6}s$ 。在 $t = 0$ 时, 产生过剩载流子的外部作用停止,因此 $t > 0$ 时半导体恢复到平衡状态, $t = {4\mu s}$ 时的过剩载流子的复合率 $( {1.83} \times {10}{19}{\mathrm{cm}}{-3}{\mathrm{s}}^{-1})$ 。
解: 首先考虑连续性方程:
$$
\begin{align}
\frac{\partial \Delta n}{\partial t} = D_{n} \frac{\partial^{2} \Delta n}{\partial x^{2}} - \mu_{n}E\frac{\partial \Delta n}{\partial x} - \mu_{n} n \frac{\partial E}{\partial t} -\frac{\Delta n}{\tau} +g_{p}
\end{align}
$$
其中 $t = 0$ 时外部作用停止,故 ${g}_{p} = 0$ ; 且 $t > 0$ 时半导体恢复至平衡状态,故过剩载流子均匀分布,即 $\frac{\partial {\Delta n}}{\partial x} = 0$ ; 同时电场强度 $E = 0$ ,故上式化简为:
$$
\begin{align}
\frac{\partial \Delta n}{\partial t} = -\frac{\Delta n}{\tau}
\end{align}
$$
解得:
$$
\begin{align}
\Delta n = \Delta n(t=0) e^{-\frac{t}{\tau}}
\end{align}
$$
故过剩载流子的复合率等于单位时间内过剩载流子数量的减少量, 即:
$$
\begin{align}
U=-\frac{d \Delta n}{d t}= \frac{\Delta n(t=0)}{\tau} e^{-\frac{t}{\tau}}
\end{align}
$$
代入$\Delta n=10{15}cm{-3}$,$\tau_{n0}=10^{-6}s$,$t=4\mu s$得:
$$
\begin{align}
U=\frac{10^{15} cm^{-3} }{10^{-6}s}\cdot e^{-\frac{4\mu s}{1\mu s}}=1.83\times 10^{19} cm{-3}s{-1}
\end{align}
$$
3. 假设两块半导体材料 $\mathrm{A}$ 和 $\mathrm{B}$ 除了禁带宽度不同,其它参数完全相同。 $\mathrm{A}$ 的禁带宽度是 ${1.0}\mathrm{eV}$ , B 的禁带宽度是 ${1.2}\mathrm{eV},{300}\mathrm{K}$ 时两种材料的 ${n}_{i}$ 的比值是 (46.812)。
解:考虑
$$
\begin{align}
n_{i} = N_{C} N_{V} e^{-\frac{E_{g}}{2k_{0}T}}
\end{align}
$$
故有:
$$
\begin{equation}
\begin{aligned}
\frac{n_{iA}}{n_{iB}} &= \frac{\exp(-\frac{E_{gA}}{2k_{0}T})}{\exp(-\frac{E_{gB}}{2k_{0}T})} \
&=\exp(\frac{E_{gB}-E_{gA}}{2k_{0}T}) \
&=\exp(\frac{0.2eV}{2 \times 0.026eV}) \
&=46.812
\end{aligned}
\end{equation}\
$$
4. 特定半导体内存在三种散射机制,只存在一种散射机制时的迁移率为 $\mu_{1}=2000cm^{2}/(V\cdot s)$ ,只存在第二种散射机制时的迁移率为 $\mu_{2}=1500cm^{2}/(V\cdot s)$ ,只存在第三种散射机制时的迁移率为 $\mu_{1}=2000cm^{2}/(V\cdot s)$ ,只存在二种散射机制时的迁移率为 $\mu_{3}=500cm^{2}/(V\cdot s)$ ,总的迁移率为( $\quad$ )
解: 考虑载流子迁移率和散射概率之间满足:
$$
\begin{align}
\mu = \frac{q\tau}{m^{\ast}} = \frac{q}{m^{\ast}P}
\end{align}
$$
其中 $\tau$ 为相邻两次散射之间的平均自由时间, $p$ 为散射概率。其中载流子的散射总概率满足:
$$
\begin{align}
&{P}{sum} = {P}{I} + {P}{II} + {P}{III} + \ldots \
&\frac{1}{\tau_{sum} } = \frac{1}{\tau_{I}} + \frac{1}{\tau_{II} } + \frac{1}{ \tau_{III} } + \ldots \
&\frac{1}{\mu_{sum} } = \frac{1}{\mu_{I} } + \frac{1}{\mu_{II} } + \frac{1}{\mu_{III} } + \ldots
\end{align}
$$
其中 ${P}{I},{P}{II},{P}{III}$ 分别表示不同散射机制的散射概率,对应的 ${\tau }{I},{\tau }{I},{\tau }{I}$ 是对应散射机制的平均自由运动时间,对应的 ${\mu }{I},{\mu }{I},{\mu }_{I}$ 是对应散射机制的载流子迁移率。
故代入本题数据得:
$$
\begin{align}
\frac{1}{\mu_{sum} } &= \frac{1}{\mu_{1} } + \frac{1}{\mu_{2} } + \frac{1}{\mu_{3}} \notag\
&= \frac{1}{2000} + \frac{1}{1500} + \frac{1}{1500} \
\Rightarrow \mu_{sum} &= 316 cm^{2}/(V\cdot s)
\end{align}
$$
5. 最有利效的复合中心能级位置在 (D) 附近; 最有利陷阱作用的能级位置在 © 附近, 常见的是 (E) 陷阱。
A. ${E}{A};$ B. ${E}{D};$ C. ${E}{F};$ D. ${E}{i};$ E. 少子 F. 多子
解:
- 最有效的复合中心能级位于禁带中央附近即 ${E}{i}$ 附近,若假设 ${r}{n} = {r}_{p} = r$ ,则
$$
\begin{align}
U = \frac{N_{t} r (np - n_{i}^{2})}{n+p+2n_{i} ch(\frac{E_{t}-E_{i}}{k_{0}T})}
\end{align}
$$
当且仅当 ${E}{t} = {E}{i}$ 时上式的分母最小,即复合率最大,故此时复合中心最有效。
-
最有效的陷阱作用的能级位于费米能级附近即 ${E}{F}$ 附近,因为费米能级以下的能级已经被填充满, 起不到俘获电子的作用; 若能级费米能级以上, 则其上的电子容易在热激发的作用下回到导带,起不到俘获电子的作用,故最有效的陷阱作用的能级位于费米能级附近即 ${E}{F}$ 附近。其中常俘获少子。
-
杂质能级的这种积累非平衡载流子的作用就称为陷阱效应, 故陷阱能级主要俘获非平衡少数载流子, 即主要为少子能级。
6. 当一种 $\mathrm{n}$ 型半导体的少子寿命由直接辐射复合决定时,其小注入下少子寿命正比于(A)。
A. $\frac{1}{ {n}{0} };$ B. $\frac{1}{\Delta n};$ C. $\frac{1}{ {p}{0} };$ D. $\frac{1}{\Delta p}$
解: 考虑直接复合的少子寿命满足:
$$
\begin{align}
\tau = \frac{1}{r(n_{0} + p_{0} + \Delta p )}
\end{align}
$$
对于 $\mathrm{n}$ 型半导体在小注入条件下有:
$$
\begin{align}
n_{0} \gg p_{0} , n_{0} \gg \Delta p
\end{align}
$$
故有:
$$
\begin{align}
\tau \sim \frac{1}{rn_{0} }
\end{align}
$$
故少子寿命正比于 $\frac{1}{ {n}_{0} }$ 。
7. 以下 4 种半导体最适合制作高温器件的是 (D)。
解: 若半导体器件的禁带宽度越宽,则该器件的极限工作温度越高; 本征载流子浓度 ${n}_{i}$ 满足下式:
$$
\begin{align}
n_{i} = \left[ \frac{2(2\pi k_{0} T)^{\frac{2}{3}} (m_{n}^{\ast} m_{p}^{\ast} )^{\frac{3}{4}} }{\hbar^{3}} \right] exp(-\frac{E_{g} }{2k_{0}T})
\end{align}
$$
半导体器件正常工作指的是本征载流子浓度至少比杂质浓度第一个数量级,故 ${n}{i}$ 越小,则器件的极限工作温度越高; 从上式可以发现 ${E}{g}$ 越大就可以实现越小的 ${n}_{i}$ ,即可以实现更高的极限工作温度。
其中 Si、Ge、GaAs、GaN 的禁带宽度分别为:1.12eV、0.6643eV、1.42eV、3.44eV;故 GaN 最适合做高温器件。
二、根据对 (Si) 晶体结构基本认识, 尝试回答以下问题: (10 分)
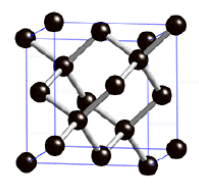
- 试画出 $\mathrm{Si}$ 的晶体结构图;
解: $\mathrm{Si}$ 的晶体结构图如下图所示
- 试比较 (100)、(110) 和 (111) 面密度的大小, 要求写出详细计算过程; 解: 其中各晶向如下图所示:
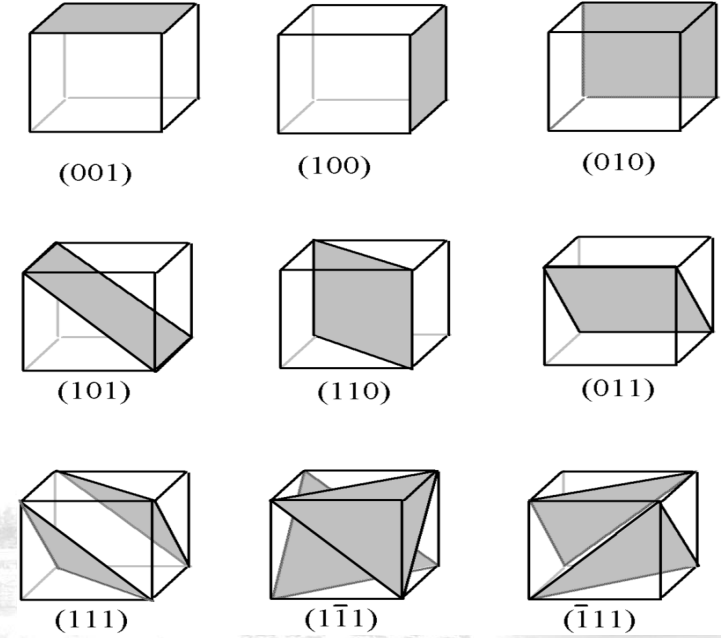
- (100) 晶面
(100) 晶面上的原子分布情况如下: 4 个顶点各有一个原子, 面心一个原子, 所以 (100) 晶面上的原子数为:
$$
\begin{align}
\text{原子数}=1+4\times \frac{1}{4} = 2
\end{align}
$$
乘积因子的解释:其中面心的原子为该晶面独占;顶点的四个原子分别同另外三个 **其他晶胞的 (100) 晶面 **共用,所以算原子数时需要乘 $\frac{1}{4}$ 。
同时 (100) 晶面的面积为:
$$
\begin{align}
\text{(100)晶面面积} = a^{2} =(5.43\times 10{-8}\mathrm{cm}){2}
\end{align}
$$
所以 (100) 晶面的原子面密度为:
$$
\begin{align}
\text{(100)晶面原子面密度} &= \frac{2}{(5.43\times 10{-8}\mathrm{cm}){2}} \
&= 6.78\times 10^{14} \mathrm{cm}^{-2}
\end{align}
$$
- (110) 晶面
(110) 晶面上的原子分布情况如下:4 个顶点各有一个原子;上下棱的棱心各有一个原子;面上有原晶胞的体对角线上的两个原子, 所以 (110) 晶面上的原子数为:
$$
\begin{align}
\text{原子数}=2+4\times \frac{1}{4} +2\times \frac{1}{2} = 4
\end{align}
$$
乘积因子的解释:其中面上的 2 个原子为该晶面独占;顶点的四个原子分别同另外三个 其他晶胞的(110)晶面 共用,所以算原子数时需要乘 $\frac{1}{4}$ ;上(下) 棱的棱心的原子分别与正上 (下) 方的一个 晶胞的 (110) 晶面共用,所以算原子数时需要乘 $\frac{1}{2}$ 。
同时 (110) 晶面的面积为:
$$
\begin{align}
\text{(110)晶面面积} = a\times \sqrt{2}a =\sqrt{2}(5.43\times 10{-8}\mathrm{cm}){2}
\end{align}
$$
所以 (110) 晶面的原子面密度为:
$$
\begin{align}
\text{(110)晶面原子面密度} &= \frac{4}{\sqrt{2}(5.43\times 10{-8}\mathrm{cm}){2}} \
&= 9.62\times 10^{14} \mathrm{cm}^{-2}
\end{align}
$$
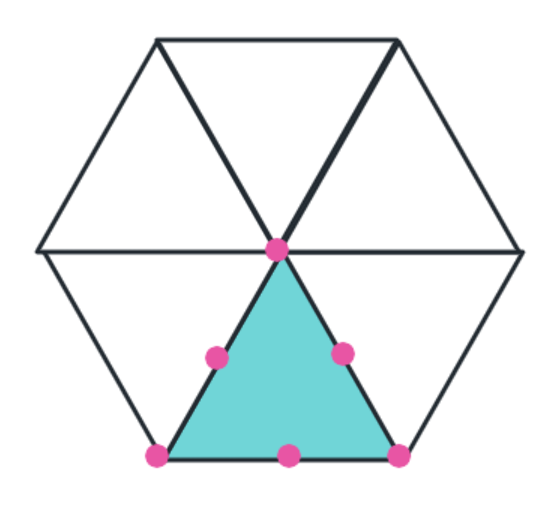
- (111) 晶面
(111) 晶面上的原子分布情况如下: 三角形的 3 个顶点各有一个原子, 三角形的三条边分别有一个原子 (原晶胞的三个面心上的原子):
$$
\begin{align}
\text{原子数}=3\times \frac{1}{6}+3\times \frac{1}{2} = 2
\end{align}
$$
乘积因子的解释: 三角形的 3 个顶点的原子如下图所示分别同另外六个其他晶胞的 (111) 晶面共用,所以算原子数时需要乘 $\frac{1}{6}$ ; 边上的原子分别同另外一个晶胞的 (111) 晶面共用,所以算原子数时需要乘 $\frac{1}{2}$ 。
同时 (111) 晶面的面积为:
$$
\begin{align}
\text{(111)晶面面积} = \frac{\sqrt{3}}{4} (\sqrt{2}a)^{2} =\frac{\sqrt{3}}{2}(5.43\times 10{-8}\mathrm{cm}){2}
\end{align}
$$
所以 (111) 晶面的原子面密度为:
$$
\begin{align}
\text{(111)晶面原子面密度} &= \frac{2}{\frac{\sqrt{3}}{2}(5.43\times 10{-8}\mathrm{cm}){2}} \
&= 7.84\times 10^{14} \mathrm{cm}^{-2}
\end{align}
$$
3.MOSFET 器件和 NPN 晶体管制造过程中, 会分别选用那种晶向的衬底, 为什么?
解:
- MOS 管常用 (100) 晶向的晶圆来制作器件。
-
MOSFET 的工作电流为表面多子的漂移电流, 其大小与载流子的表面迁移率 (mobility) 有关, 其中 (100) 晶向的界面态密度最低, 表面迁移率最高, 可以使 MOSFET 有较高的工作电流。
-
(100) 晶向的较低的界面态和悬挂键可以减小 MOSFET 的阈值电压 ${V}_{TH}$ 。
-
(100) 晶向的缺陷密度最低,可以减小 ${V}_{TH}$ 的漂移。
-
(100) 晶向粒子扩散速度慢, 有利于 MOSFET 较小氧化层厚度的生长。
- BJT 管常用 (111) 晶向的晶圆来制作器件。
-
BJT 的工作电流是少子体扩散电流, 与表面迁移率关系较小。
-
(111) 晶向的原子最多 (原子面密度最大), 可以增大场阈电压, 为 BJT 提供较好的纵向载流子迁移率。
-
(111) 晶向的缺陷密度高,适合用来提高 BJT 中的寄生 PMOS 管的 ${V}_{TH}$ 。
-
利用 (111) 晶向可以更精确的控制基区宽度。
-
(111) 晶向的粒子扩散速度快, 考虑到 BJT 中的高掺杂特性, 扩散速度快可以减少 BJT 的制作时间。
三、谈根据所学知识, 谈谈你对晶体中缺陷的认识。(10 分)
解: 晶体缺陷即是实际晶体偏离理想结构的不完整区域, 其分为如下三类:
i) 点缺陷:空位、间隙
晶格原子由于热振动脱离平衡位置获得足够的能量而离开周围原子的束缚, 挤入晶格原子的间隙,形成间隙原子;同时原位置成为空位;这种间隙和空位成对出现的缺陷称为弗仑克尔缺陷。 当只在晶体中形成空位时, 称为肖特基缺陷。
ii) 线缺陷:位错
位错包括刃位错和螺位错两种, 前者位错线垂直于滑移方向 (伯氏矢量), 而后者位错线平行于滑移方向。特别地, 刃位错包含 Glide 和 Climb 两种。
iii) 面缺陷:晶界、亚晶界、相界
晶界是多晶材料中, 两种晶体或晶粒之间的交界面。通常在腐蚀开始处或新相在母相的出溶处形成, 并使得材料的电学性能和热学性能降低。
缺陷的存在会使严格按周期性排列的原子所产生的周期性势场受到破坏, 有可能在近代中引入能级,进而对半导体的性质产生决定性影响。
四、讨论杂质浓度和温度分别对禁带宽度、迁移率、电阻率的影响。(10 分) 解:
- 杂质浓度和温度对半导体禁带宽度的影响:
随着杂质浓度的升高, 杂质原子之间靠得更近, 导致杂质原子之间的电子波函数发生重叠, 使孤立的杂质能级扩展为能带, 常称为杂质能带, 特别的若杂质能带进入了导带或价带, 并与导带或价带相连, 则形成了新的简并能带, 使能带的状态密度发生了变化, 简并能带的尾部伸入禁带,形成带尾。导致禁带宽度由 $\mathrm{E}\mathrm{g}$ 减小为 $\mathrm{E}$ ’ $\mathrm{g}$ ,禁带宽度变窄。
考虑 Varshni 模型, 温度与禁带宽度之间满足:
$$
\begin{align}
E_{g}(T) = E_{g}(0) - \frac{\alpha T^{2}}{\beta + T}
\end{align}
$$
常见的半导体如 $\mathrm{Si}$ 和 $\mathrm{Ge}$ 的禁带宽度具有负温度系数,但特别地锑化铟的 ${E}_{g}$ 具有正温度系数。
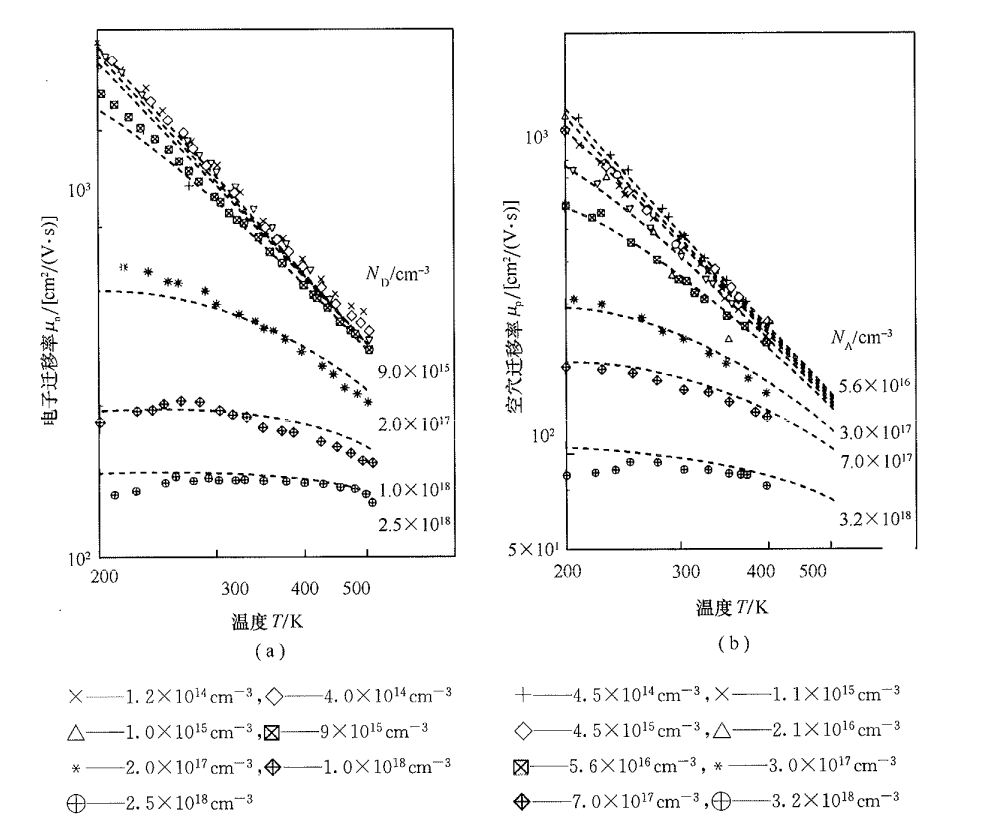
- 杂质浓度和温度对半导体迁移率的影响:
硅中电子迁移率和空穴迁移率与杂质浓度和温度的关系如下图所示:
若只考虑电离杂质散射和声学波散射,则载流子迁移率 $\mu$ 服从:
$$
\begin{align}
\mu = \frac{q}{m^{\ast}} \cdot \frac{1}{A T^{\frac{2}{3}} + \frac{BN_{i}}{T^{\frac{2}{3}}}}
\end{align}
$$
故从图 4 和式 (2.30) 中均可得到如下结论:随着温度的升高, 载流子迁移率降低; 同时随着杂质浓度的升高, 载流子迁移率降低。但当杂质浓度较大时, 低温区域内载流子迁移率会随着温度升高有小幅度的增加, 而后随着温度的升高而降低。
杂质浓度很高的 $\mathrm{n}$ 型硅,由于施主能级扩展成杂质能带,导致禁带变窄,导带中运动的电子除受到电离杂质的散射外, 还会被施主能级所俘获, 这些被俘获的电子经过一定的时间还会被释放到导带中参与导电, 这些电子在导带中做漂移运动时, 不断地被施主能级俘获, 再释放, 再俘获, 使得电子的漂移运动减慢, 此外一些杂质带中的电子由于杂质原子轨道重叠, 也可能在施主原子间运动, 而不参与导电, 因此导带中有相当一部分电子在杂质带上运动, 从而迁移率有所降低。
- 杂质浓度和温度对半导体电阻率的影响:
若只考虑电离杂质散射和声学波散射, 则半导体电阻率、电导率与载流子迁移率存在如下关系 (以 $\mathrm{n}$ 型半导体为例):
$$
\begin{equation}
\begin{aligned}
\rho &= \frac{1}{\sigma} \
\sigma &= n \mu_{n} q\
\Rightarrow \rho &= \frac{m^{\ast}}{q} \frac{A T^{\frac{2}{3}} + \frac{BN_{i}}{T^{\frac{2}{3}}}}{ nq }
\end{aligned}
\end{equation}
$$
故硅的电阻率随杂质浓度、温度的变化如下图所示:
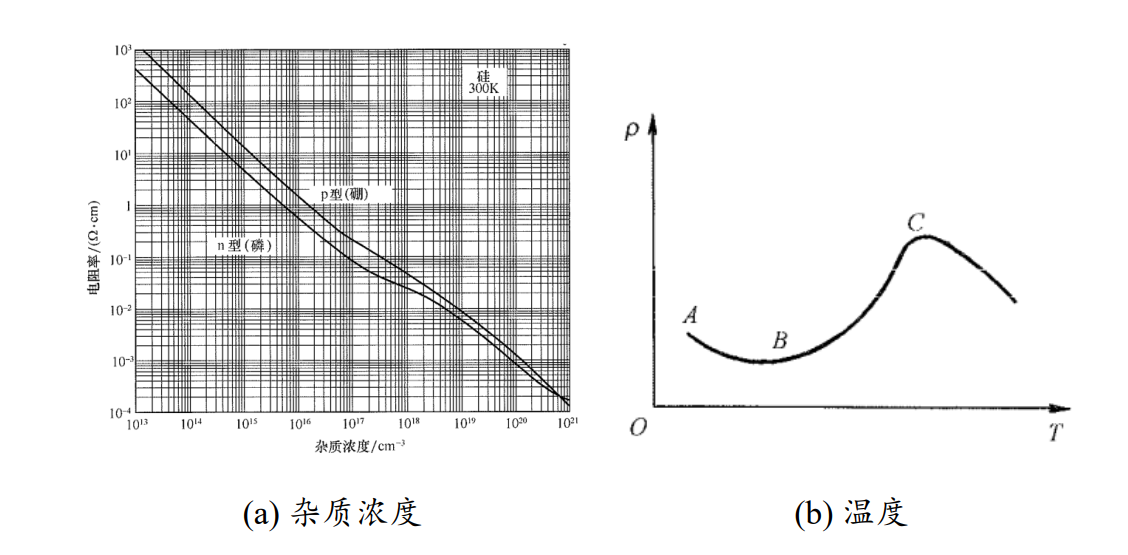
故随着杂质浓度的升高, 器件电阻率降低; 随着温度的升高, 器件电阻率先下降再升高再下降。
五、描述直接复合与间接复合的物理过程。为什么只有深能级才能起到有效复合中心的作用? 说明掺 $\mathrm{Au}$ 后寿命为什么会明显下降?(10 分) 解:
直接复合即导带中的电子直接落入价带与空穴复合。间接复合即非平衡载流子通过复合中心的复合。若假设 ${r}{n} = {r}{p} = r$ ,则
$$
\begin{align}
U = \frac{N_{t} r (np - n_{i}^{2})}{n+p+2n_{i} ch(\frac{E_{t}-E_{i}}{k_{0}T})}
\end{align}
$$
故从上式得到如下结论: 当且仅当 ${E}{t} = {E}{i}$ 时上式的分母最小,即复合率最大,故位于禁带中央附近的复合中心能级最有效。
掺入金后,在 $\mathrm{Si}$ 中形成了深能级的复合能级,是有效的复合中心。其中 $\mathrm{n}$ 型硅的少子寿命满足:
$$
\begin{align}
\tau_{p} = \frac{1}{N_{t}r_{p}}
\end{align}
$$
故随着金浓度 ${N}_{t}$ 的增大,少子寿命等比例的减小,故少量的有效复合中心就能大大缩短少子寿命。
六、何谓少子寿命?决定半导体少子寿命的主要因素有哪些,并说明原因?写出三种或三种以上少子寿命检测的方法, 并简要说明基本测试原理 (15 分) 解:
少子寿命即载流子两次相邻散射之间的平均自由运动时间,或者是载流子复合率的倒数。
影响半导体少子寿命的主要有:复合能级位置、复合中心浓度、俘获系数、温度、器件的杂质浓度。
少子寿命检测方法:
- 直流光电导衰减法
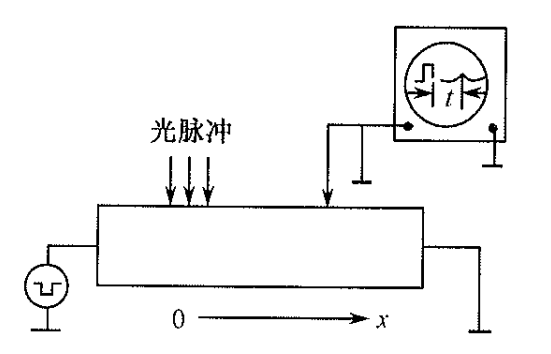
基于下式
$$
\begin{align}
\Delta p(t) = \Delta p(0)\cdot e^{-\frac{t}{\tau}}
\end{align}
$$
测量电导率衰减为峰值的 $\frac{1}{e}$ 时的时间即可测得少子寿命
- 霍尔效应法
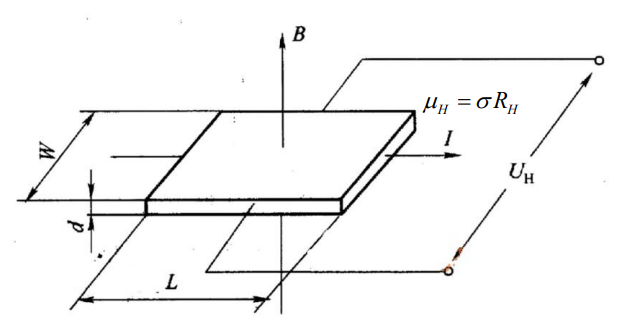
基于下式:
$$
\begin{equation}
\begin{aligned}
E_{H} &= \frac{R_{H}IB}{A}\
R_{H} &= -\frac{1}{nq} \
\mu_{H} &= \sigma R_{H}
\end{aligned}
\end{equation}
$$
通过测量电导率衰减为峰值的 $\frac{1}{e}$ 时的时间即可测得少子寿命
- 微波光电导衰减法 参考资料
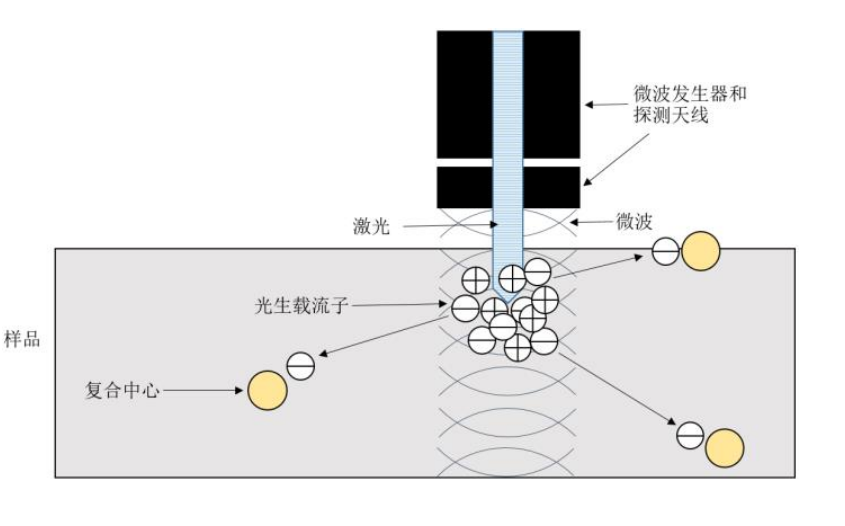
由于微波信号的变化量正比于电导率的变化量, 从而可以通过探测微波反射信号来探测电导率的变化, 得到样品的载流子寿命。
七、一 $\mathrm{n}$ 型半导体样品,复合能级 ${E}{t}$ 在导带底之下三分之一 ${E}{g}$ 处,设 ${\tau }{n}$ 和 ${\tau }{p}$ 为同一数量级, 并且与温度无关。试根据复合中心理论讨论寿命与温度的关系, 并根据得出的结果, 说明复合中心能级 ${E}_{t}$ 位置的方法。(25 分)
解:
则根据直接复合理论,非平衡载流子的复合率 $\mathrm{U}$ 可以表示为:
$$
\begin{align}
U = \frac{ r_{n}(n_{0}+n_{1}) + r_{p}(p_{0}+p_{1}) }{ N_{t} r_{p}r_{n}(n_{0}+p_{0}) }
\end{align}
$$
其中
$$
\begin{equation}
\left{
\begin{aligned}
n_{0} &=N_{C} \mathrm{exp}(\frac{E_{F}-E_{C}}{k_{0}T}) , &n_{1}=N_{C} \mathrm{exp}(\frac{E_{t}-E_{C}}{k_{0}T})\
p_{0} &=N_{V} \mathrm{exp}(\frac{E_{V}-E_{F}}{k_{0}T}), &p_{1}=N_{V} \mathrm{exp}(\frac{E_{V}-E_{t}}{k_{0}T})
\end{aligned}
\right.
\end{equation}
$$
其中硅中金的空穴俘获截面的典型值满足下式:数据出处
$$
\begin{equation}
\left{
\begin{aligned}
\sigma_{P} &=(3.7\pm 0.7)\times 10^{-15} (\frac{300}{T})^{2.9\pm 0.3} \mathrm{cm}^{2}, &T\in (150K,200K) \
\sigma_{P} &=(1.4\pm 0.3)\times 10^{-15} (\frac{300}{T})^{2} \mathrm{exp} (-\frac{19 meV}{k_{0}T}) \mathrm{cm}^{2}, &T\in (160K,318K)\
\sigma_{P} &=(2.3\pm 0.3)\times 10^{-15} (\frac{300}{T})^{1.2\pm 0.2} \mathrm{cm}^{2}, &T\in (77K,180K)
\end{aligned}
\right.
\end{equation}
$$
故电子俘获截面 ${\sigma }{ - }$ 和空穴俘获截面 ${\sigma }{ + }$ 与温度之间的关系近似满足:
$$
\begin{align}
\sigma \sim T^{-n} , n \in(2,4)
\end{align}
$$
若考虑电子俘获率和空穴俘获率满足下式:
$$
\begin{equation}
\left{
\begin{aligned}
r_{p} &=\sigma_{P} V_{T} &\
r_{n} &=\sigma_{n} V_{T} &\
V_{T} &=\sqrt{\frac{3k_{0}T}{m^{\ast}}} &
\end{aligned}
\right.
\end{equation}
$$
则式 (2.39) 可变换成下式:
$$
\begin{align}
U = \frac{\sigma_{+}\sigma_{-}V_{T}N_{t}(np-N_{c}N_{v}\mathrm{exp}(-\frac{E_{g}}{k_{0}T}))}{\sigma_{-}\left[ n + (N_{c}N_{v})^{\frac{1}{2}} \mathrm{exp}(-\frac{5E_{g}}{6k_{0}T}) \right] + \sigma_{+}\left[ p + (N_{c}N_{v})^{\frac{1}{2}} \mathrm{exp}(-\frac{7E_{g}}{6k_{0}T}) \right] }
\end{align}
$$
其中 ${N}{c}$、${N}{v}$ 满足:
$$
\begin{equation}
\left{
\begin{aligned}
N_{c} &=2(\frac{m_{n}^{\ast} k_{0} T }{2\pi \hbar{2}}){\frac{3}{2}} &\
N_{v} &=2(\frac{m_{p}^{\ast} k_{0} T }{2\pi \hbar{2}}){\frac{3}{2}} &
\end{aligned}
\right.
\end{equation}
$$
则 (2.40) 可近似等价为:
$$
\begin{align}
U \sim \frac{T^{\alpha-\frac{3}{2}} ( np - T^{3}\mathrm{exp}(-\frac{E_{g}}{k_{0}T})) }{n+T^{\frac{3}{2}} \mathrm{exp}(-\frac{E_{g}}{k_{0}T}) \mathrm{ch}(\frac{E_{g}}{6k_{0}T}) } , \alpha\in (0,1)
\end{align}
$$
但该式子 $U$ 与 $T$ 的关系图较难绘制,故通过如下方式考虑简化式子来讨论。
根据参考资料我们有全温度范围内的硅的费米能级变化, 同时该图像考虑了禁带宽度随温度增加的变化的 varish 模型, 是较为准确的数据。
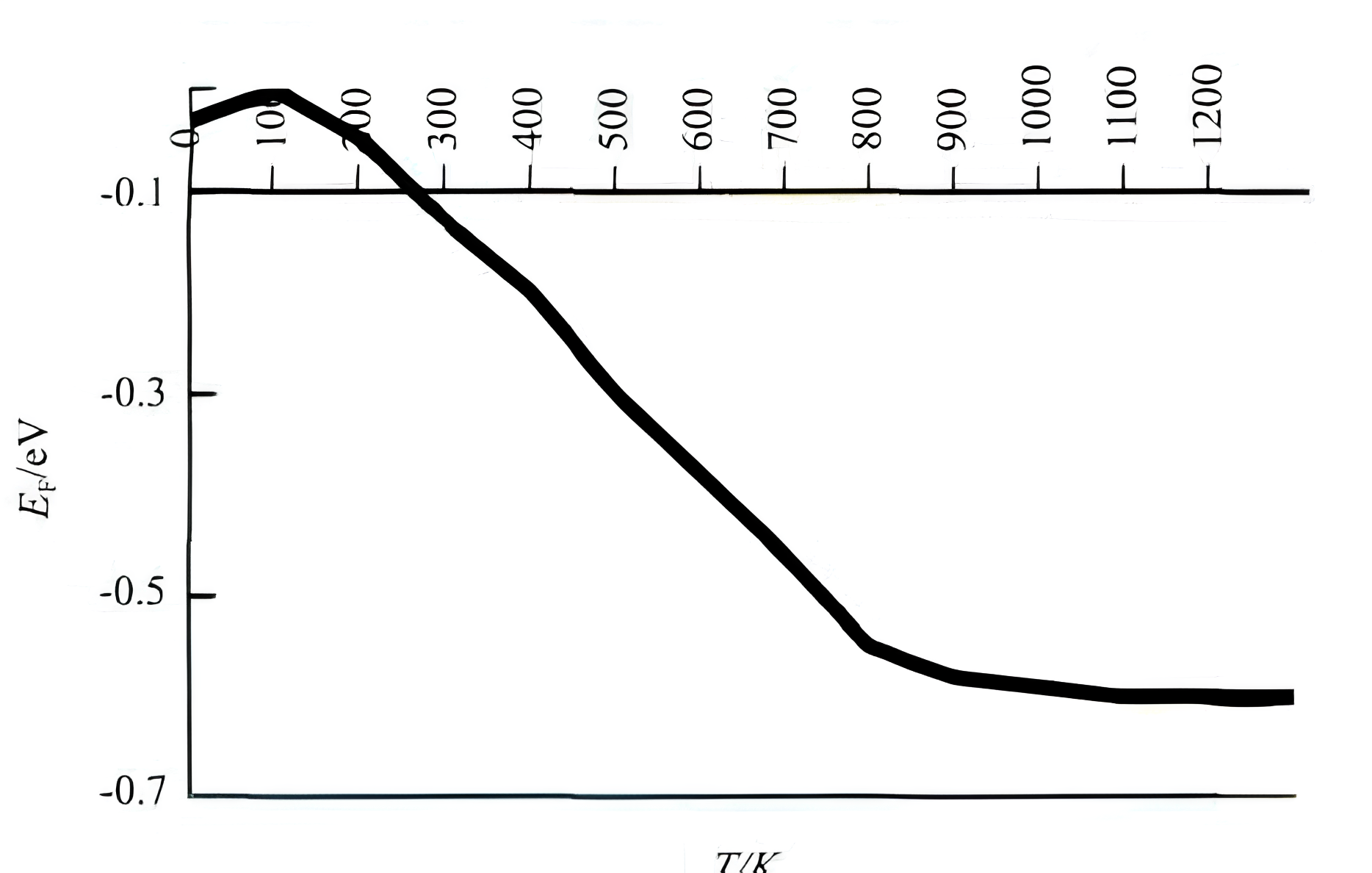
故从较大的温度范围内来看, 硅的费米能级随温度的变化满足下述规律:
-
在温度 ${0K} < T < {100K}$ 的低温弱电离区间, 费米能级随温度的升高而逐渐增大。温度约为 ${100}\mathrm{K}$ 时,最大费米能级位于导带底以下 ${0.059}\mathrm{eV}$ 处。
-
在温度 ${100K} < T < {700K}$ 范围内,费米能级几乎呈线性下降。
-
温度大于 ${700}\mathrm{K}$ 时,费米能级逐渐趋于平缓,接近带隙中间,即本征半导体的费米能级。
同时由于 ${E}{t} - {E}{i} = \frac{ {E}{g} }{6} = {0.187}\mathrm{ {eV} }$ ,故可根据图 9 所示的 ${E}{F}$ 变化曲线近似估计少子寿命 $\tau$ 的变化。
新文献结果补充:
![用SRH复合模拟Si样品过量载流子衰变[3]](https://www.helloimg.com/i/2024/12/27/676e8251dca9c.png)
可利用载流子浓度衰减为峰值的 $\frac{1}{e}$ 所需的时间来估计少子寿命。
![p型硅样品的高、低注入寿命值和高、低注入寿命之比随温度的变化曲线[4]](https://www.helloimg.com/i/2024/12/27/676e8252a177a.png)
参考文献
[1] 陈开茅,毛晋昌,晏懋洵,吴恩,曾奇勇. 硅中金的空穴俘获截面的研究. 北京大学物理系, 1983.
[2] 王惠,杨伟强,严金梅,魏红军. 关于 $\mathrm{N}$ 型晶体硅费米能级的研究. 晶澳太阳能有限公司,2015.
[3] Johnston S, Ahrenkiel R K. Measurement of the temperature dependence of silicon recombination lifetimes[J]. MRS Online Proceedings Library (OPL), 1998, 510: 607.
[4] Johnston S W, Ahrenkiel R K. Measurement of the temperature-dependent recombination lifetimes in photovoltaic materials[C]//AIP Conference Proceedings. American Institute of Physics, 1999, 462(1): 505-510.